An S4 Class implementing Laplacian Eigenmaps
Details
Laplacian Eigenmaps use a kernel and were originally developed to separate non-convex clusters under the name spectral clustering.
Slots
funA function that does the embedding and returns a dimRedResult object.
stdparsThe standard parameters for the function.
General usage
Dimensionality reduction methods are S4 Classes that either be used
directly, in which case they have to be initialized and a full
list with parameters has to be handed to the @fun()
slot, or the method name be passed to the embed function and
parameters can be given to the ..., in which case
missing parameters will be replaced by the ones in the
@stdpars.
Parameters
LaplacianEigenmaps can take the following parameters:
- ndim
the number of output dimensions.
- sparse
A character vector specifying hot to make the graph sparse,
"knn"means that a K-nearest neighbor graph is constructed,"eps"an epsilon neighborhood graph is constructed, else a dense distance matrix is used.- knn
The number of nearest neighbors to use for the knn graph.
- eps
The distance for the epsilon neighborhood graph.
- t
Parameter for the transformation of the distance matrix by \(w=exp(-d^2/t)\), larger values give less weight to differences in distance,
t == Inftreats all distances != 0 equally.- norm
logical, should the normed laplacian be used?
Implementation
Wraps around spec.emb.
References
Belkin, M., Niyogi, P., 2003. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Computation 15, 1373.
Examples
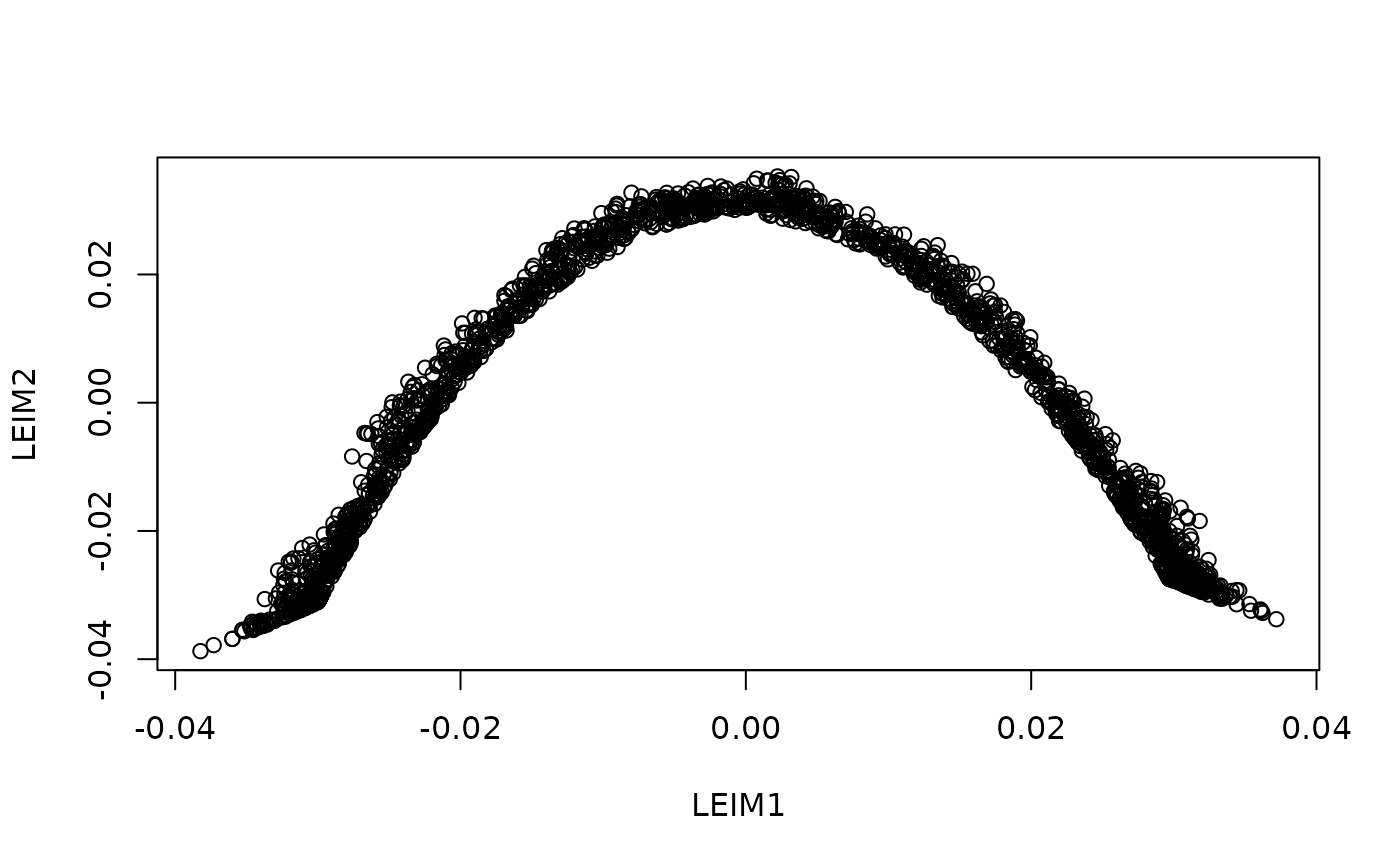
if(requireNamespace(c("loe", "RSpectra", "Matrix"), quietly = TRUE)) {
dat <- loadDataSet("3D S Curve")
emb <- embed(dat, "LaplacianEigenmaps")
plot(emb@data@data)
}
#> 2023-03-21 13:05:26: Creating weight matrix
#> 2023-03-21 13:05:26: Eigenvalue decomposition
#> Eigenvalues: 1.039229e-02 2.605511e-03 -4.539080e-17
#> 2023-03-21 13:05:26: DONE